Masters thesis topics
Computational Quantum Many-Body Physics
Context
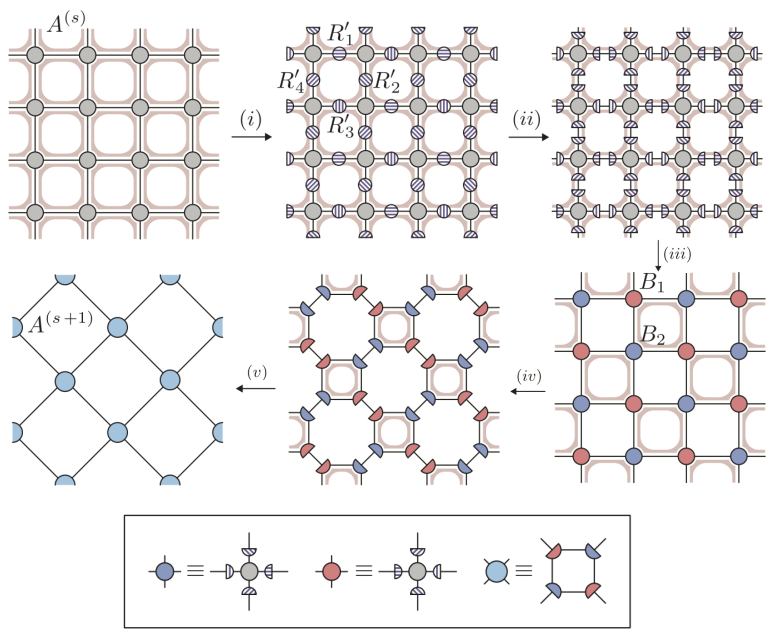
The renormalisation group (RG) is one of the cornerstones of modern theoretical physics and exists in various implementations across different areas of classical as well as quantum physics. One particularly insightful RG scheme in the context of classical spin models in statistical mechanics is Kadanoff’s spin blocking [1], a particular example of a real-space coarse-graining scheme [2]. While very instructive, this particular scheme does not result in a quantitatively precise description of critical phenomena. More recently, highly accurate real-space coarse-graining schemes have been constructed using the formalism of tensor networks. Hereto, the partition function of a statistical or quantum mechanical system is represented as a network of contracted tensors, where the contractions between different tensor indices encode the summations over the configuration space variables. By decomposing these tensors and contracting them, real-space transformations are obtained that result in coarse grained partition functions in terms of novel statistical variables. After the initial proposal by Levin and Nave [3], different improved and more advanced schemes have been proposed [4,5,6] (one of which is depicted below), and various strategies have been developed to extract the scaling behaviour of the system from these numerical simulations [7,8].
This technique can also be applied to quantum systems with fermionic degrees of freedom, which are then encoded using Grassmann numbers [9]. In the last one year, this approach has been reproduced using the formalism of fermionic super vector spaces[10] in the context of tensor based RG. Moreover, tensor based RG methods have been used to study Lattice gauge theories (LGTs) which normally cannot be studied using conventional methods. Thus tensor networks are a promising approach in the long term goal of simulating Lattice QCD. Many open questions remain:
-
For quantum field theories on a lattice there are different ways to encode the partition function as a tensor network. Extending this formalism to Hamiltonians or actions with both fermionic and dynamical gauge degrees of freedom in (1+1) and (2+1) dimensions is of particular interest as ultimately QCD has both fermions and gauge bosons. How to encode continuous gauge degrees of freedom using symmetric tensors and efficiently represent and then contract the tensor network for the partition function remains an open question.
-
There are different numerical tensor renormalisation schemes that can be used to study these theories from the simplest one proposed by Levin and Nave to more complicated state-of-the-art ones such as Loop-TNR which can capture the RG flow in much better detail. Implementing these algorithms for fermionic and gauge degrees of freedom is of particular interest.
-
Finally, calculating observable quantities such as local observables, Wilson Loops and their expectation values with tensor networks is of great interest as these objects are important for studying the different phases of a lattice field theory.
Goal
The goals of these thesis is to address the points raised above and can depend on the interest of the student. We will start with replicating some of the existing results from fermionic tensor-based RG (TRG) studies, thereby translating the Grassmann number formalism to super vector spaces. We have developed an open-source Julia software package to perform Tensor Network Renormalisation (TNR) simulations called TNRKit.jl. A part of this project can also be to further develop this software library by adding novel TNR schemes. Next, we will look at the different strategies to discretise the fermionic and gauge degres of freedom to efficiently represent the lattice partition function as a tensor network and study different LGTs using the available TNR schemes. Finally, if time permits, we will implement and investigate algorithms to measure observables and study the critical spectra of different models.
[1] Kadanoff, L. P. (1966). Scaling laws for Ising models near T c. Physics Physique Fizika, 2(6), 263.
[2] Efrati, E., Wang, Z., Kolan, A., & Kadanoff, L. P. (2014). Real-space renormalization in statistical mechanics. Reviews of Modern Physics, 86(2), 647. arXiv:1301.6323.
[3] Levin, M., & Nave, C. P. (2007). Tensor renormalization group approach to two-dimensional classical lattice models. Physical review letters, 99(12), 120601. arXiv:cond-mat/0611687.
[4] Xie, Z. Y., Chen, J., Qin, M. P., Zhu, J. W., Yang, L. P., & Xiang, T. (2012). Coarse-graining renormalization by higher-order singular value decomposition. Physical Review B, 86(4), 045139. arXiv:1201.1144.
[5] Evenbly, G., & Vidal, G. (2015). Tensor network renormalization. Physical review letters, 115(18), 180405. arXiv:1412.0732.
[6] Hauru, M., Delcamp, C., & Mizera, S. (2018). Renormalization of tensor networks using graph-independent local truncations. Physical Review B, 97(4), 045111. arXiv:1709.07460.
[7] Gu, Z. C., & Wen, X. G. (2009). Tensor-entanglement-filtering renormalization approach and symmetry-protected topological order. Physical Review B, 80(15), 155131. arXiv:0903.1069.
[8] Ueda, A., & Oshikawa, M. (2023). Finite-size and finite bond dimension effects of tensor network renormalization. arXiv preprint arXiv:2302.06632.
[9] Gu, Z. C., Verstraete, F., & Wen, X. G. (2010). Grassmann tensor network states and its renormalization for strongly correlated fermionic and bosonic states. arXiv preprint arXiv:1004.2563.
[10] Bultinck, N., Williamson, D. J., Haegeman, J., & Verstraete, F. (2017). Fermionic matrix product states and one-dimensional topological phases. Physical Review B, 95(7), 075108. arXiv:1610.07849.
Context
In recent years, cold atom experiments world-wide have rapidly claimed their position at the forefront of the remarkable advances taking place in our understanding of the quantum world. Such endeavours routinely push the boundaries of experimentally accessible regimes and uncover novel quantum phenomena, necessitating the advancement of ab-initio numerical techniques to understand these systems. Despite the popularity and effectiveness of tensor network techniques in simulating quantum systems, they have not seen many significant applications in these kinds of cold atom setups, aside from the setting of optical lattices.
In order to use tensor networks on such continuous systems, it is necessary to construct a network of local Hilbert spaces, effectively encoding the system on a lattice. However, a naive approach of discretizing the spatial dimension to generate a grid (i.e. finite differences) scales poorly with the number of grid points and introduces convergence issues during the variational optimization [1]. A common alternative involves expanding the wave-function with respect to a set of global basis functions (i.e. spectral methods) that are chosen based on the geometry and boundary conditions of the system. While these generally have excellent convergence properties, they introduce highly non-local terms in the Hamiltonian which invalidates the usual entanglement considerations that tensor network states are based upon.
A promising middle-ground seems to exist in the form of Discrete Variable Representations (DVR) [2], closely related to Pseudo-spectral methods. This approach amounts to the construction of a localized basis set through the application of an appropriate transformation on a spectral basis set. This allows the evaluation of local potentials on a discrete grid, while only introducing a slightly non-local kinetic energy term in the Hamiltonian. As a result, the DVR method is expected to maintain locality to a good extent as with grid-based methods, while also possessing similar convergence properties as spectral methods, giving us the best of both worlds. Such an approach has significant potential as it opens up the possibility of studying inhomogenous cold atom systems in the continuum.
[1] Michele Dolfi, Bela Bauer, Matthias Troyer, and Zoran Ristivojevic, Multigrid Algorithms for Tensor Network States, https://arxiv.org/abs/1203.6363
[2] John C. Light, Tucker Carrington Jr., Discrete Variable Representations and their Utilization, http://light-group.uchicago.edu/dvr-rev.pdf
Goal
The overall goal of this thesis is to understand the utility and limitations of Discrete Variable Representations in augmenting tensor network techniques (particularly, matrix product states) to study strongly interacting one-dimensional systems in the continuum. This will be largely facilitated by gaining familiarity with the numerical tensor network toolbox [3] developed by our group.
Over the course of the project, the student will develop modular numerical routines that facilitates experimentation with various DVRs to discretize the continuum, followed by the application of tensor network machinery to study the system. This will involve performing benchmarks with an alternative discretization scheme that has been explored recently [4], based on dividing the continuous space into segments and choosing carefully tuned basis functions within each of them (akin to finite element methods). Based on the results of these attempts, a motivated student may also wish to explore natural extensions to higher dimensions. This project is well-suited for a student with a strong interest in computational physics and in the development of efficient numerical techniques.
[3] MPSKit.jl, https://quantumghent.github.io/software/
[4] Shovan Dutta, Anton Buyskikh, Andrew J. Daley, Erich J. Mueller, Density-Matrix Renormalization Group for Continuous Quantum Systems, https://arxiv.org/abs/2108.05366
Context
An intriguing property of a large class of many-body lattice systems is the emerging local scale invariance at their critical points where a phase transition occurs. At these points, it is understood that the low-energy physics can be captured by conformal field theories (CFTs). Various challenges arise when it comes to modelling the critical behavior of these strongly correlated systems. One approach to modelling these critical lattice models is via a tensor network (TN) representation of their partition function [1]. In our research group we have developed a plethora of numerical algorithms and a numerical toolbox to optimize and renormalize these tensor networks [2].
Through the lens of tensor network renormalization [4,5], ref. [3] proposed a method to extract the local observables of a CFT, known as the primary operators. The method relies on a tensor network representation of the (discrete) local rescaling operator on the level of the partition function.
Goal
The goal of this thesis is study the approach of ref. [3] to CFT operators on the lattice, incorporate it in our toolbox and conduct state-of-the art research with the developed code.
The student would first familiarize themselves with the numerical tensor network toolbox developed in our group [2]. They would then reproduce the results of [3,4,5] and benchmark the codebase. Subsequently the student can improve upon the results of in several ways. One avenue which can be pursued would be to compute correlation functions involving the found primary operators. The student could also investigate how the so-called topological symmetries of the conformal models can be incorporated.
The project will be carried out in an international research environment. This project is well-suited for students with a keen interest in mathematical physics and numerical simulations.
[1] J. I. Cirac, D. Pérez-García, N. Schuch, F. Verstraete - arXiv:2011.12127
[2] Software page
[3] G. Evenbly, G. Vidal - arXiv:1510.00689
[4] G. Evenbly, G. Vidal - arXiv:1412.0732
[5] G. Evenbly - arXiv:1509.07484
Context
The Bose-Einstein condensate (BEC) is a phase of matter, consisting of many (+10.000) interacting ultra-cold bosonic atoms in the quantum regime. The collective quantum many-body nature of the BEC gives rise to peculiar emergent behavior, admitting topologically non-trivial excitations such as vortices and solitons, linked to superfluidity. Solitons are localized waves that propagate without losing their shape thanks to the balance between nonlinear and dispersive effects in a medium. They can be observed in various situations such as shallow water, fiber optics and, indeed, superfluids. It is the latter context that we want to explore with this thesis.
Already in 2000, 5 years after the first creation of a BEC, solitons were generated in these systems, see Ref [1]. The procedure consisted of laser-imprinting an appropriate phase difference onto the BEC wavefunction. In recent years, the spectacular advances in experimental techniques have facilitated a higher degree of control and manipulation of atomic gases enabling more finetuned protocols. In Ref [2] they demonstrate a technique to create more versatile soliton-settings, paving the way to study more involved soliton-physics such as multiple solitons interacting.
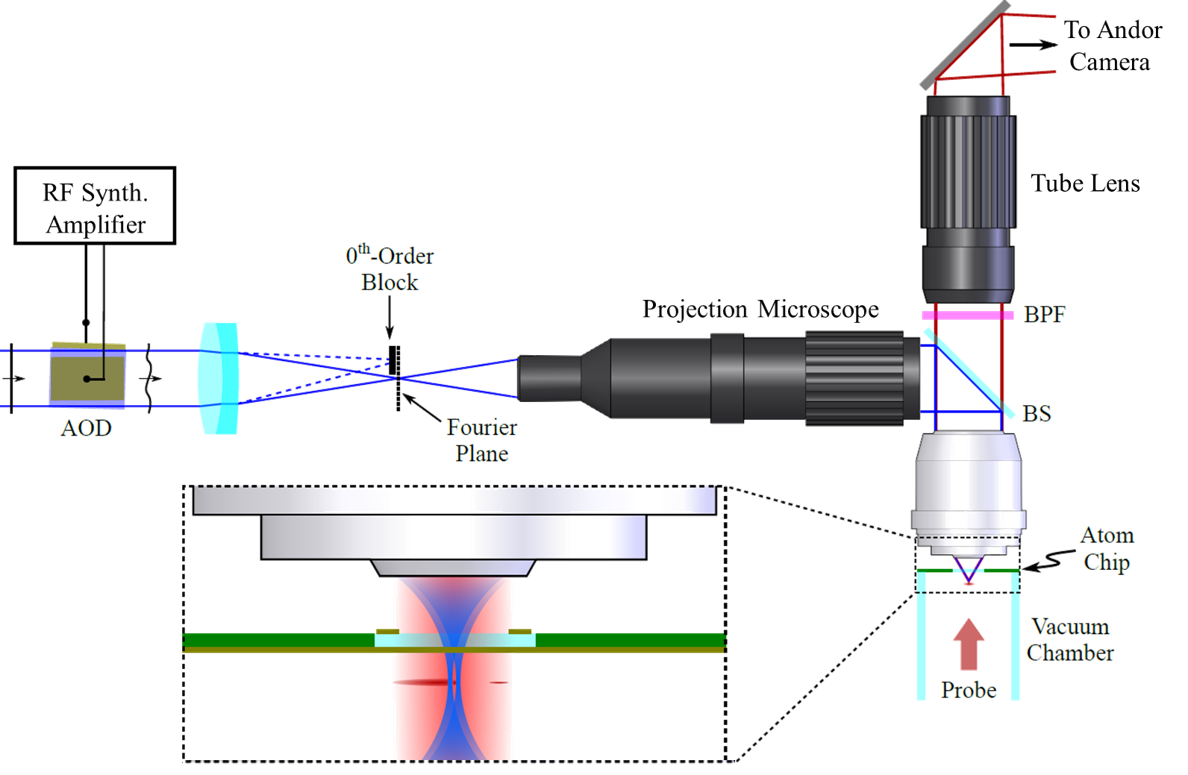
Since 2022, our group hosts a state-of-the-art experiment where BECs can be manipulated with programmable laser light and magnetic fields.
![Example soliton from [2]](/images/thesistopics/2025/CTanghe1.png)
[1] J. Denschlag et al. Generating Solitons by Phase Engineering of a Bose-Einstein Condensate.Science 287,97-101(2000). doi:10.1126/science.287.5450.97
[2] Fritsch, A. R. and Lu, Mingwu and Reid, G. H. and Pineiro, A. M. and Spielman, I. B. Creating solitons with controllable and near-zero velocity in Bose-Einstein condensates. Phys. Rev. A 101, 053629 (2020). doi:10.1103/PhysRevA.101.053629
Goal
The goal of the thesis is to study and engineer methods as described in Ref [2] in our own lab with the aim to create solitons at arbitrary position and velocity. As such, the student has the opportunity to develop and apply numerical methods and quantum optics theory on a cutting-edge quantum experiment.
The student will start by familiarizing themselves with the theoretical description of solitons in BECs. Using existing numerical packages, example experiments can be simulated. Once the physics behind the protocol is understood, the student will adapt it to our experimental set-up. Since our system uses a different light-shaping technique, namely Acousto Optic Deflectors (AODs) instead of Digital Micromirror Devices (DMDs) as in Ref [2], the student will engineer different optimal protocols suited to the actual experiment.
This thesis draws from different fields: quantum optics, quantum field theory, numerical analysis and cold atom physics. As the thesis fits within a larger research goal of our group, depending on their interests and skills the student will have the freedom to focus more on the theoretical, numerical or experimental part of the project.
Context
High-temperature superconductivity was first discovered in 1986 when a system of barium, lanthanum, copper, and oxide exhibited a critical temperature of 30K—then the highest recorded. However, BCS theory, the original framework for superconductivity, failed to explain this phenomenon. A complete theory of this effect is still missing, more than 40 years after its discovery.
To study and simulate superconductivity, the Hubbard model was introduced as a minimal model. It describes fermions hopping on a (in the case of the cuprates: square) lattice, with a hopping term and a repulsive term [1]
\(H = -t \sum_{<i j> \sigma} \left(\hat{c}_{i \sigma}^\dagger \hat{c}_{j \sigma} + h.c.\right) + U \sum_i \hat{n}_i \hat{n}_j\).
However, solving it remains a significant challenge, leading to the development of numerous computational approaches. Among these, Tensor Networks (TN) have emerged as a powerful tool, explicitly capturing strong correlations without suffering from the sign problem (like Quantum Monte Carlo methods). In particular, the two-dimensional TN variant, Projected Entangled-Pair States (PEPS), is widely used but has been primarily applied to ground-state (0K) calculations and static properties. To get more insight into the Hubbard model, it is crucial to extend these methods to finite-temperature states and their time evolution [2].
A key computational challenge in the latter is evaluating the exponential of the Hamiltonian. For finite temperatures, this requires computing the density operator:
\[\rho(\beta) = e^{-\beta H}\]Since this is exponentially hard in the system size, approximations are necessary. The traditional approach relies on the Suzuki-Trotter decomposition, but a more recent and accurate alternative is to use cluster expansions (see Figure 1) [3,4].
Goal
This thesis will explore different methods for probing the finite-temperature phase diagram of the Hubbard model. There are multiple directions that could be taken depending on the interests of the student. One possibility is implementing a new algorithm based on the Suzuki-Trotter decomposition and comparing it with the existing cluster expansion code, or by using the purification instead of the thermal density operator [5]. Another is using cluster expansions to study various parameter regimes of the Hubbard model, looking both at the feasibility and computational cost of obtaining accurate results. Further optimizations to enhance efficiency may also be considered. These methods will allow us to look at the finite-temperature phase diagram of the Hubbard model (see Figure 2).
[1] Qin M. (2021) arxiv:2104.00064
[2] Sinha A. (2022) arxiv:2209.00985
[3] Vanhecke B. (2021) arxiv:2112.01507
[4] Vanhecke B. (2019) arxiv:1912.10512
[5] Czarnik P. (2018) arxiv:1811.05497
Context
Superconductors have vanishing electrical resistance under a certain temperature, called the critical temperature Tc. They were first discovered by the Dutch physicist Heike Kamerlingh Onnes in 1911, when he found that mercury exhibits superconductivity with Tc = 4.2K [1]. Thus began the search for materials exhibiting superconductivity at room temperature. A big step in this search was the discovery of high-temperature superconductivity in 1986 [2]. Here, they found a critical temperature of 30K, the highest at the time, for a system consisting of barium, lanthanum, copper, and oxide, specifically BaxLa5−xCu5O5(3−y) with x = 1 and 0.75 and y > 0. The original theory to describe superconductivity proposed by Bardeen, Cooper, and Schrieffer, called BCS theory, failed to describe this high-temperature superconductivity [3, 4]. A complete theory of this effect is still missing, more than 40 years after its discovery.
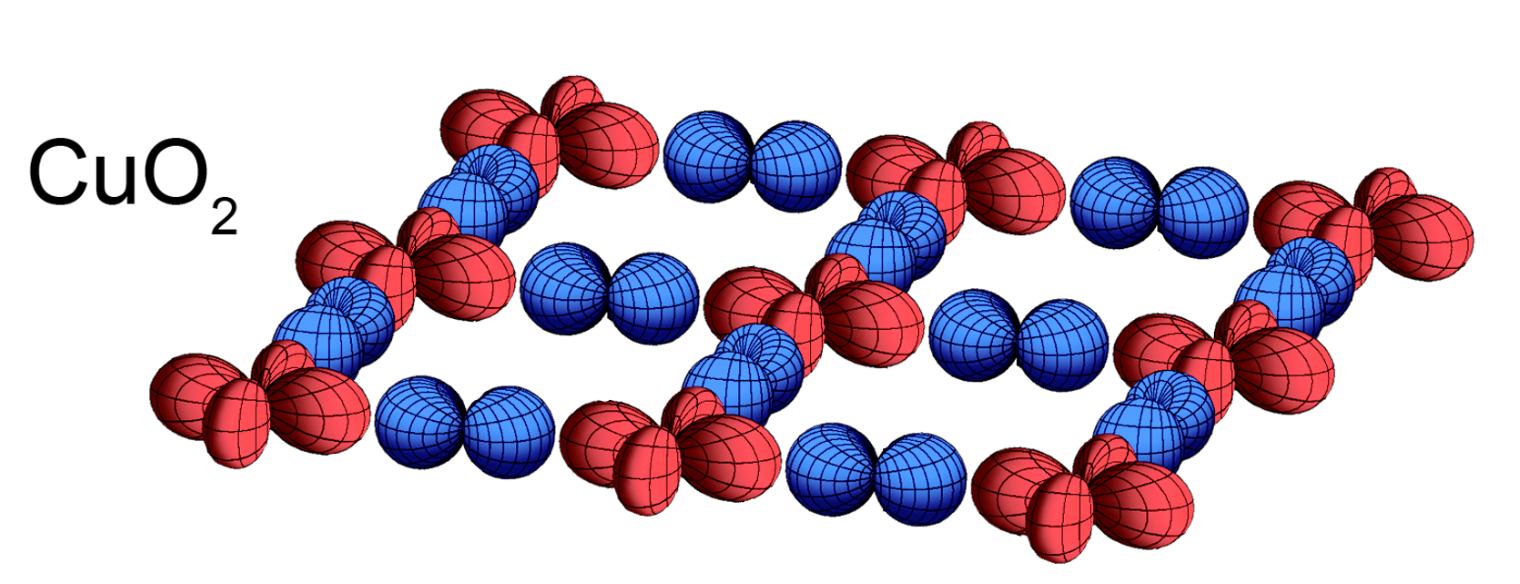
Goal
The goal is to start from a Density-Funtional Theory calculation of the material HgBa2CuO4 (Figure 1) and to capture the strongly correlated degrees of freedom with a downfolding procedure. This yields an effective Hamiltonian that can be solved using Tensor Networks [5,6]. The student can either perform a calculation of the Hubbard model or the t-J model based on the desired balance between accuracy and computational cost. The ground state wave function can then be found using the 2-dimensional version of tensor networks, called Projected Entangled-Pair States (PEPS). The student can look whether this ground state is superconducting or exhibits stripe-order to probe the zero-temperature phase diagram (Figure 2) [7]. The next step could be to not only incorporate interactions that act between nearest neighbours on the lattice, but also include further-reaching interactions. Another extension would be look at different doping levels, to probe the influence of the electron filling on the ground state properties.

[1] Dirk, v. & Kes, P. Europhysics News 63 (2011).
[2] Bednorz, J. G. & Muller, K. A. Z. Phys. B 64, 189–193 (1986).
[3] Bardeen, J. et al. Physical Review 106, 162–164 (1957).
[4] Bardeen, J. et al. Physical Review 108, 1175–1204 (1957).
[5] Bridgeman, J. (2016) arxiv:1603.03039
[6] Vrancken, D. (2025) arxiv:2502.19588
[7] Ponsion, B. (2019) PRB:100.195141
Context
Many physically relevant objects can be expressed as infinite tensor networks. Notable examples include partition functions of 2D classical statistical mechanics models and (1+1)D quantum models. Another important case is the expectation values of Projected Entangled Pair States (PEPS), which describe 2D quantum lattice systems.
However, contracting an infinite tensor network exactly would require infinite computational resources. To address this, researchers have developed various approximate contraction techniques that achieve surprisingly high accuracy. One common approach uses the ideas of the renormalization group to perform coarse-graining on tensors within a network. These techniques are well-established and serve as a useful benchmark for this thesis.
Recently, a promising new approach has emerged, combining belief propagation with loop series expansions to approximate tensor network contractions [2, 3].
- Effectively compressing and optimizing tensor networks requires reliable methods for fixing the latent degrees of freedom of the tensors, known as the gauge. One such method is called Belief Propagation [2].
- Loop series expansions build upon belief propagation by expressing the tensor network contraction as a series expansion, making otherwise intractable contractions feasible [4].

Goal
This thesis will take a numerical approach, requiring implementation in the Julia programming language. It consists of three main objectives:
- Implement belief propagation for square tensor networks using the TensorKit package, a Julia library developed by the quantum group that provides essential tools for tensor network calculations.
- Utilize loop series expansions to contract infinite square tensor networks.
- Benchmark the method against existing contraction techniques, evaluating both numerical accuracy and computational efficiency.
The student will have the freedom to explore alternative approaches for loop series expansions and is encouraged to develop novel algorithms through creative experimentation.
References
[1] Bridgeman, J. (2016) arxiv.org:1603.03039
[2] Tindall, J. (2023) arxiv.org:2306.17837
[3] Evenbly, G. (2024) arxiv.org:2409.03108
[4] Tindall, J. (2024) arxiv.org:2306.14887
Context
The Algebraic Bethe Ansatz (ABA) stands as one of the most significant exact methods in quantum integrable systems [1,2], providing analytical solutions to a wide class of many-body problems that would otherwise remain intractable. Despite its theoretical elegance and exactness, the ABA presents significant computational challenges when applied to the calculation of physical observables. Given these computational challenges, it is desirable to have an efficient numerical method to calculate the physical quantities of interest from Bethe ansatz wave functions. One promising direction is to exploit the matrix product state (MPS) representation of the Bethe ansatz wave function [3,4]. In Ref.[4], it was demonstrated that by applying standard matrix product state techniques, one can successfully truncate the bond dimension of the exact MPS to numerically manageable sizes while maintaining good accuracy for various observables. However, significant challenges emerge if this method is applied to larger systems, as the truncation process encounters substantial entanglement barriers that affect numerical accuracy.
Goal
This master thesis project aims to address these limitations by developing a novel computational approach that combines Monte Carlo sampling techniques with tensor network representations of Bethe ansatz wave functions. The proposed research includes developing efficient Monte Carlo sampling algorithms tailored to the MPS representation of Bethe eigenstates, implementing and benchmarking these methods for computing correlation functions and other physical observables, comparing the performance with traditional truncation approaches in terms of accuracy and computational efficiency. The student will gain a solid understanding of both the theoretical framework of algebraic Bethe ansatz and several numerical techniques, including tensor network algorithms and Monte Carlo sampling methods [5,6]. This knowledge will position the student for further research either on improving traditional tensor network algorithms or developing VMC+PEPS algorithms for challenging two-dimensional quantum systems.
References
[1] L. D. Faddeev, arXiv:hep-th/9404013 [2] L. D. Faddeev, arXiv:hep-th/9605187 [3] H. Katsura, I. Maruyama, arXiv:0911.4215 [4] V. Murg, V. E. Korepin, F. Verstraete, arXiv:1201.5627 [5] Ling Wang, Iztok Pizorn, Frank Verstraete, arXiv:1010.5450 [6] W.-Y. Liu, S. J. Du, R. Peng, J. Gray, G. K.-L. Chan, arXiv: 2405.03797
Context
In classical circuit, one can use a series of binary code (i.e., ‘0’ and ‘1’) to represent the information and use logic gate to realize all kinds of operations. While in quantum circuit, the binary code is replaced by the quantum state (i.e., ‘|0>’ and ‘|1>’ in Fock space) and the gate operation becomes local unitary evolution. From a product state, the system can generate long-range entanglement after a long enough unitary evolution, while the measurement (local Hermitian projection) could reduce it. Thus, one should expect there is a Measurement-Induced Phase Transitions (MIPT) [1-3]. However, most of the recent quantum circuit research focus on the bosonic states and operations (i.e., hard core bosons) and fermionic quantum circuit which shares the same Hilbert space seems less attractive. The reason can come from the redundancy of Jordan-Wigner string in a matrix product operator (MPO) which is the main tool used. If one is familiar with the Projective Quantum Monte Carlo (PQMC) [5], he/she should find out it is a perfect tool to study fermionic quantum circuit since there is an isomorphic mapping. The decoupled repulsive interaction corresponds to the unitary evolution, and the kinetic term becomes the Hermitian projection. The interesting observations in bosonic quantum circuit like MIPT should also be expected in a fermionic quantum circuit with a potentially different critical behavior.
Goal
The goal of this thesis is to explore the possibility of simulating a fermionic quantum circuit within PQMC framework. A first step could be comparing the one-dimensional critical behavior of MIPT between fermionic and bosonic random quantum circuit. Due to PQMC has no dimensional limitation from entanglement area law, one can also study the critical behavior in higher dimension (e.g., two-dimension) fermion quantum circuit.
References
[1] Fisher, M.P., Khemani, V., Nahum, A. and Vijay, S., arXiv:2207.14280 [2] Skinner B, Ruhman J, Nahum A., arXiv:1808.05953 [3] Li Y, Chen X, Fisher M.P., arXiv:1808.06134 [4] Li Y, Chen X, Fisher M.P., arXiv:1901.08092 [5] F Assaad, H Evertz, Computational many-particle physics
Condensed Matter Physics
Context
At the heart of quantum many-body physics lies a deep question: how does collective behavior emerge from individual particle properties? A rather fundamental example is how a collection of elementary fermions —whether spatially delocalized Cooper pairs in superconductors, strongly bound protons and neutrons in ultracold alkali atoms, or paired fermionic atoms in superfluid He3— can effectively exhibit macroscopic quantum coherence. Despite their diverse physical realizations, these systems share a common feature: under suitable conditions, a composite entity comprised of elementary fermions can effectively behave as bosons. However, this is just an approximation that is expected to break down when the composite particles overlap significantly, as observed in exciton condensates. There are then two natural questions that arise: Can we define a quantitative measure of compositeness that sets a strict criterion for when an entity can truly be treated as a boson? And when this condition fails, how does the statistics of the internal structure manifest in the deviation from ideal bosonic behavior? While it is now well known that the validity of treating a bound pair as a single elementary entity is not solely dictated by strong interactions but rather by the preservation of entanglement between its constituents [1], the precise manner in which this compositeness affects measurable quantities remains an unexplored question.
Goal
This project aims to systematically explore the compositeness effects of bosons by formulating a 1D lattice model of interacting fermions with tunable interaction strengths, similar to Ref [2]. While Ref [2] examined the conditions under which a collection of 2N fermions effectively organize into N bosons of 2 particles, or N/2 bosons of 4 particles, etc, our focus will be on exploring the subsequent deviation of observable quantities like condensate density and phase coherence, and how these effects can be understood through the entanglement structure of the system. This will largely be facilitated through the use of Matrix Product State (MPS) techniques, with the possibility of incorporating an analytical perspective through the study of an integrable model, depending on the student’s interests.
[1] C. Chudzicki, et al., Entanglement and composite bosons, https://arxiv.org/abs/0908.1096
[2] Z. Lasmar, et al., Assembly of 2N entangled fermions into multipartite composite bosons, https://arxiv.org/abs/1902.08157
Context
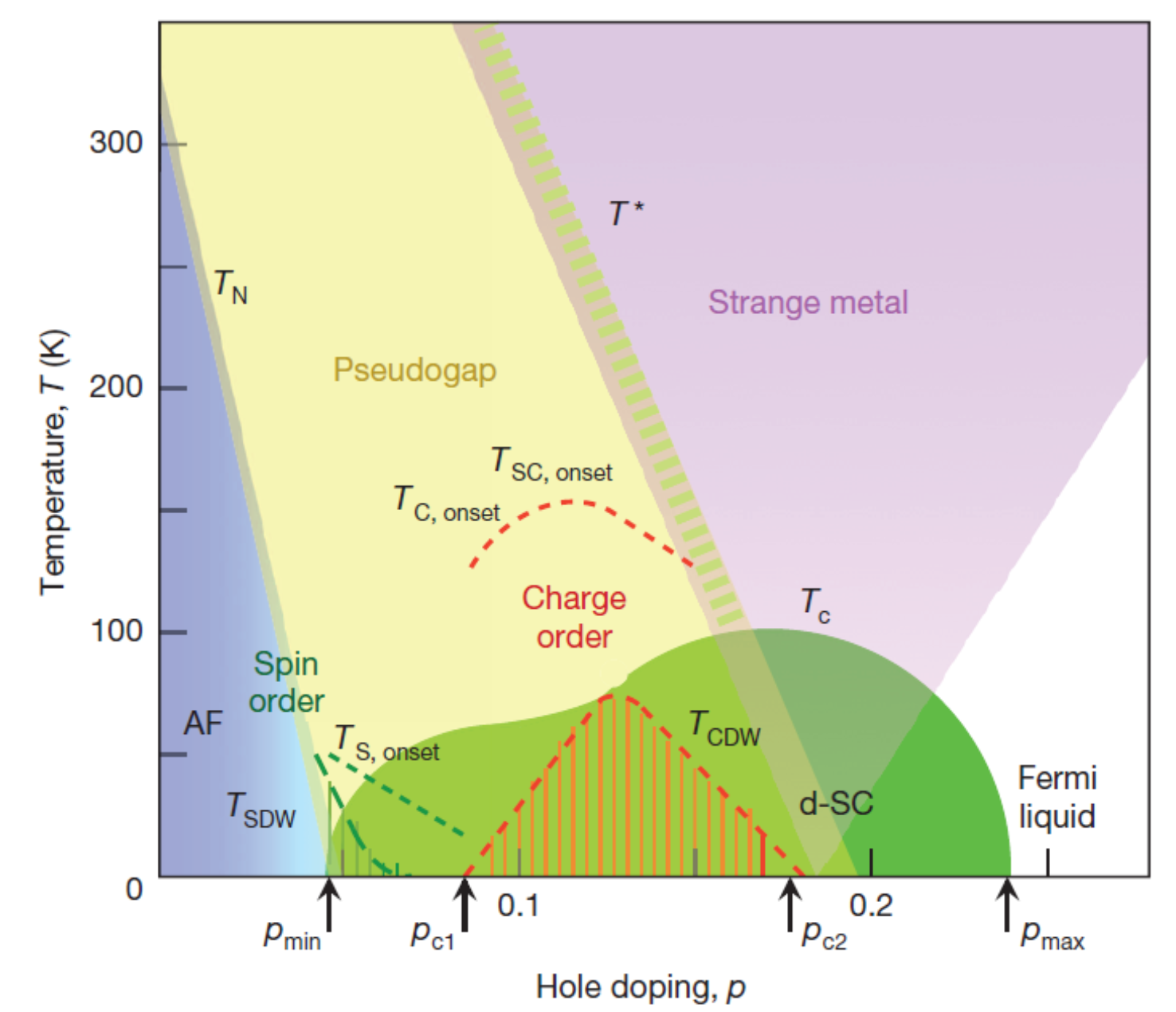
High-temperature superconductivity in cuprate materials remains one of the most intriguing, challenging, and highly debated problems in the field of condensed matter physics. Despite decades of research, the exact mechanism responsible for Cooper-pairing and the superconducting phase in these materials is still not fully understood. The cuprates exhibit a complex phase diagram characterized by a plethora of competing orders (e.g charge- and spin-density-waves, pseudogap phase, strange metal etc.), including antiferromagnetic (AFM) order [1,2]. More specifically on the electron doping side of the phase diagram, where it is strongly believed that the AFM order is the parent state for the superconducting phase, new experimental foundings suggest the unconventional pairing to be mediated through AFM spin-fluctuations, which are the finite temperature remnants of the Goldstone modes that arise in the system due to spontaneous symmetry breaking of the SU(2) spin-rotation symmetry in the AFM order [3]. Further, recent studies and theoretical proposals indicate a strong Fermi-surface reconstruction as a function of (electron-)doping. A similar reconstruction has recently been observed by thermal agitation through the appearance of a so called gossamer Fermi-surface [4]. Understanding the interplay between these phases, spontaneous symmetry breaking, and the Fermi-surface reconstruction is crucial for deciphering mysteries and understanding the fundamental nature of superconductivity in cuprates.
Goal
The goal of this project is to combine numerical as well as theoretical skills to explore the intricate connection between spontaneous symmetry breaking and superconductivity in electron-doped cuprates, as well as investigate the effects of the gossamer Fermi-surface on the superconducting phase. We explore the AFM state, which spontaneously breaks SU(2) spin-rotation symmetry, as a parent state for the superconducting phase, which is then mediated purely by AFM spin-fluctuations rather then phonons. As the parent state exhibits spontaneous symmetry breaking, the electronic system will have low-energy collective excitations corresponding to Goldstone modes of the broken symmetry (spin-fluctuations for spontaneous breaking of spin SU(2) symmetry). The student will solve for these Goldstone modes via a newly developed framework by the promoter, using a generalized random phase approximation approach and the resulting Bethe-Salpeter equation, and investigate their capability of mediating a favorable superconducting interaction [5]. In a next step the Fermi-surface reconstruction and gossamer Fermi-surface with be explored by thermal activation of virtual processes. The student will introduce Feynman diagrammatic corrections to the fermionic and bosonic propagators and investigate it’s effect on the superconducting dome, trying to make connection to recent experimental work related to the gossamer Fermi-surface, further deeping our understanding on a topic which has remained elusive for decennia.
[1] R. L. Greene, P. R. Mandal, N. R. Poniatowski, T. Sarkar, arXiv:1905.04998
[2] S. Sachdev, arXiv:2501.16417
[3] C. M. Duffy, S. J. Tu, Q. H. Chen, J. S. Zhang, A. Cuoghi, R. D. H. Hinlopen, T. Sarkar, R. L. Greene, K. Jin, N. E. Hussey, arXiv:2502.13612
[4] K. Xu, Q. Guo, M. Hashimoto, Z. Li, S. Chen, J. He, Y. He, C. Li, M. H. Berntsen, C. R. Rotundu, Y. S. Lee, T. P. Devereaux, A. Rydh, D. Lu, D. Lee, O. Tjernberg, Z. Shen, arXiv:2308.05313
[5] K. Vasiliou, Y. He, N. Bultinck, arXiv:2307.05699
Context
Classifying quantum phases of matters is one of the most significant objectives in condensed matter physics. By understanding the physical properties and their mechanisms, we can design the materials for our purposes. Yet, the macroscopic mechanism is often not obvious from the microscopic models, making it a challenging task for physicists. One strategy is to look at the phase boundaries. There, the systems often exhibit universal properties that reflect the underlying macroscopic models. The renormalisation group (RG) is an idea that captures this: we can classify universality classes of models sharing universal properties at phase boundaries, which are fixed points of RG flows.
RG flows can capture various phase transitions. In particular, fixed points of second-order phase transitions can often be described by a conformal field theory (CFT), which unlocks a powerful toolbox to understand universality classes. First-order phase transitions, on the other hand, do not show the necessary conformal invariance to accurately be captured by a CFT. However, it has been known historically that some weakly-first order phase transitions such as that of the five-state Potts model, exhibit approximate conformal invariance. Recently, such phase transitions has been shown to be still described by an analytic continuation of CFTs, called complex CFTs [2]. These have been shown to be applicable in various condensed matter/statistical physics systems, as well as in high-energy physics.
CFTs are analytically tractable in two dimensions due to conformal symmetry considerations. For this reason, most of the works in the literature studying critical lattice models do so in two dimensions. However, numerics allow us to access various conformal data in other dimensions, notably in 3D. One such development is the fuzzy sphere regularisation, which has proven to detect the fingerprints of CFTs accurately [3], and opens the gateway to realisations of various 3D CFTs. In particular, a possible connection to complex CFTs has been made with the 3-state Potts model in 2+1D [4], where the phase transition is first-order, but shows approximate conformal invariance.
Goal
This project will start off with a literature study into the relevance of complex conformal field theories in condensed matter contexts. The student will first familiarise themselves with real CFT, and how these are related to criticality and renormalisation group. Afterwards, the student is fully equipped to tackle complex CFT. Finally, the student is asked to perform some original work related to [4], which can be approached from various angles, and especially from the numerical point of view. Tensor networks, a most popular theoretical and numerical toolbox that has been developed in our research group to study strongly correlated quantum systems, will come into play on the fuzzy sphere.
The project can be tailored to the wishes and interests of the student in terms of which research topics they want to delve into.
This project is well-suited for students with a keen interest in mathematical, theoretical and computational physics. No prior knowledge on any of the mentioned topics above is required; a large part of this project concerns understanding these connections more deeply.
[1] D. Kaplan, et al., PhysRevD.80.125005
[2] V. Gorbenko, et al., arXiv:1807.11512
[3] W. Zhu, et al., PhysRevX.13.021009
[4] S. Yang, et al., arXiv:2501.14320
Context
An extremely powerful and ubiquitous concept in theoretical physics is that of duality, loosely defined as a non-trivial physical equivalence between distinct theories. The existence of a duality is typically rooted in a common mathematical structure underlying seemingly very different theories. One appeal of dualities is that certain computations that are difficult in a given theory may be much easier in a dual theory. In the context of quantum lattice models, dualities have recently been classified and constructed in terms of tensor networks in one spatial dimension [1,2], and progress has been made in (2+1)d [3,4]. This entanglement based approach to dualities has not only allowed for a concrete realization of the operators implementing the dualities explicitly on the lattice but has also led to an understanding of how quantum phases of matter can be converted into each other.
Closely related to the concept of dualities is that of non-invertible symmetries. As their name suggests these symmetries are characterized by the absence of an inverse for some of the symmetry operators, so that the resulting symmetry structure is not anymore described by a group. A systemic way of obtaining such symmetry structures is exactly via the aforementioned duality procedures.
[1] I. Cirac, D. Perez-Garcia, N. Schuch, F. Verstraete - arxiv:2011.12127
[2] L. Lootens, C. Delcamp, G. Ortiz, F. Verstraete - 2112.09091
[3] C. Delcamp, A. Tiwari - arxiv:2301.01259
[4] B. Vancraeynest-De Cuiper, C. Delcamp - arxiv:2501.16301
Goal
Recent attention has been devoted to the concept of symmetry-protected topological phases protected by non-invertible symmetries [5,6,7]. These phases are characterized by having a unique gapped ground state and, when put on open lattices, by gapless edge and interface modes. It has been shown that these phases are a particularly well-suited resource for quantum computing schemes based on measurements. The goal of this topic would be to systematically construct examples of such phases and study their properties in the tensor network framework. This project is well suited for a student with a keen interest in mathematical physics and entanglement theory.
[5] C. Fechisin, N. Tantivasadakarn, V. V. Albert - arxiv:2312.09272
[6] S. Seifnashri, S.-H. Shao - arxiv:2404.01369
[7] K. Inamura, S. Ohyama - arxiv:2408.15960
Context
This master thesis investigates tensor networks and its application to disordered spin chains. Disordered spin chains are spin chains where the coupling parameters, like magnetic field strength, are not constant but random. These systems exhibit many interesting phenomenon like power law behaviour of correlations and rare regions dominating expectation values. Tensor Network (TN) methods [1] have been pivotal in understanding the behavior of various quantum many-body systems, especially in 1D. However it remains a challenge for traditional TN approaches to simulate models with strong disorder. Recently a new tensor network algorithm has been developed by the Quantum Group at Ghent University to tackle random systems at finite temperatures in 1D. This algorithm restores the translational invariance in the disordered system by representing the density matrix as a matrix product operator (MPO), such that the power of MPO’s can be exploited. This new algorithm opens the door to new simulations of the vast realm of random spin chains.
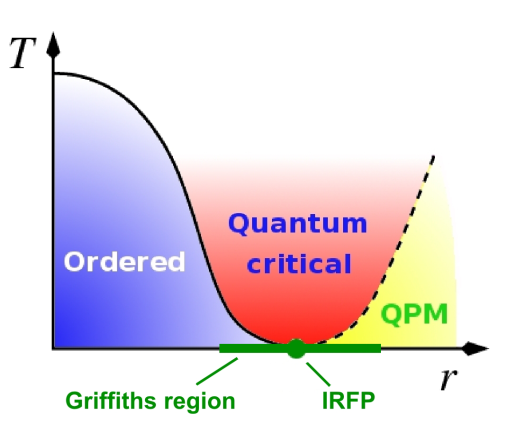
Goal
The overall goal of the thesis is to study and explore disordered quantum systems through tensor networks. The first part of the thesis consists of a literature study on tensor networks and disordered models. The student will use the tensor network toolbox developed by our group to perform novel simulations of random spin systems. Depending on the interest of the student different research directions can be pursued. One possibility is to use the existing code base to simulate a plethora of random systems and study their phase diagram. A second possibility is to optimize and benchmark the current implementation of the algorithm and extend it with symmetries. This will allow the student to tackle more challenging models like the Heisenberg model, where the exploitation of symmetries will be necessary. Thirdly the student can look into developing an analogue of the algorithm for zero temperature groundstates.
[1] J. I. Cirac, D. Pérez-García, N. Schuch, F. Verstraete, arXiv:2011.12127
Context
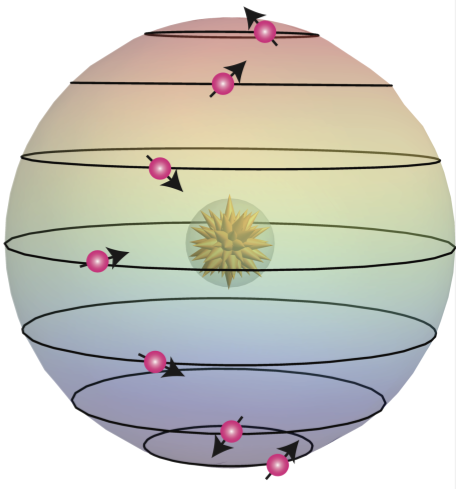
One of the ultimate goals in physics is to classify and understand all possible phases of matter. A particularly intriguing development in this program has been the discovery of topological properties in quantum systems leading to exotic phases of matter. Cold atom experiments have arisen as a powerful toolbox for exploring such phases in a highly controllable setting [1]. One interesting proposal to realise such topological phases is through the use of ’synthetic dimensions’. Here one leverages periodic driving to engineer a time-averaged Hamiltonian, a technique known as Floquet engineering, to realise a dimensional degree of freedom along the internal states of the system. The coupling along this synthetic dimension can be tuned to implement artificial gauge fields and magnetic fluxes in the system [2] thereby opening up the possibility of realising the paradigmatic quantum Hall effect.
One proposal of implementing a synthetic dimension uses a setup very similar to our BEC-lab where one ’shakes’ a harmonically trapped gas to couple the internal states along the trap [3]. The dynamics within this synthetic dimension were recently verified [4,5] and are being considered as a way to experimentally realise the paradigmatic quantum Hall effect in a non-electronic system. The technical requirements of this proposal appear to be within the reach of our future experiments, motivating a thorough exploration of its theoretical aspects.
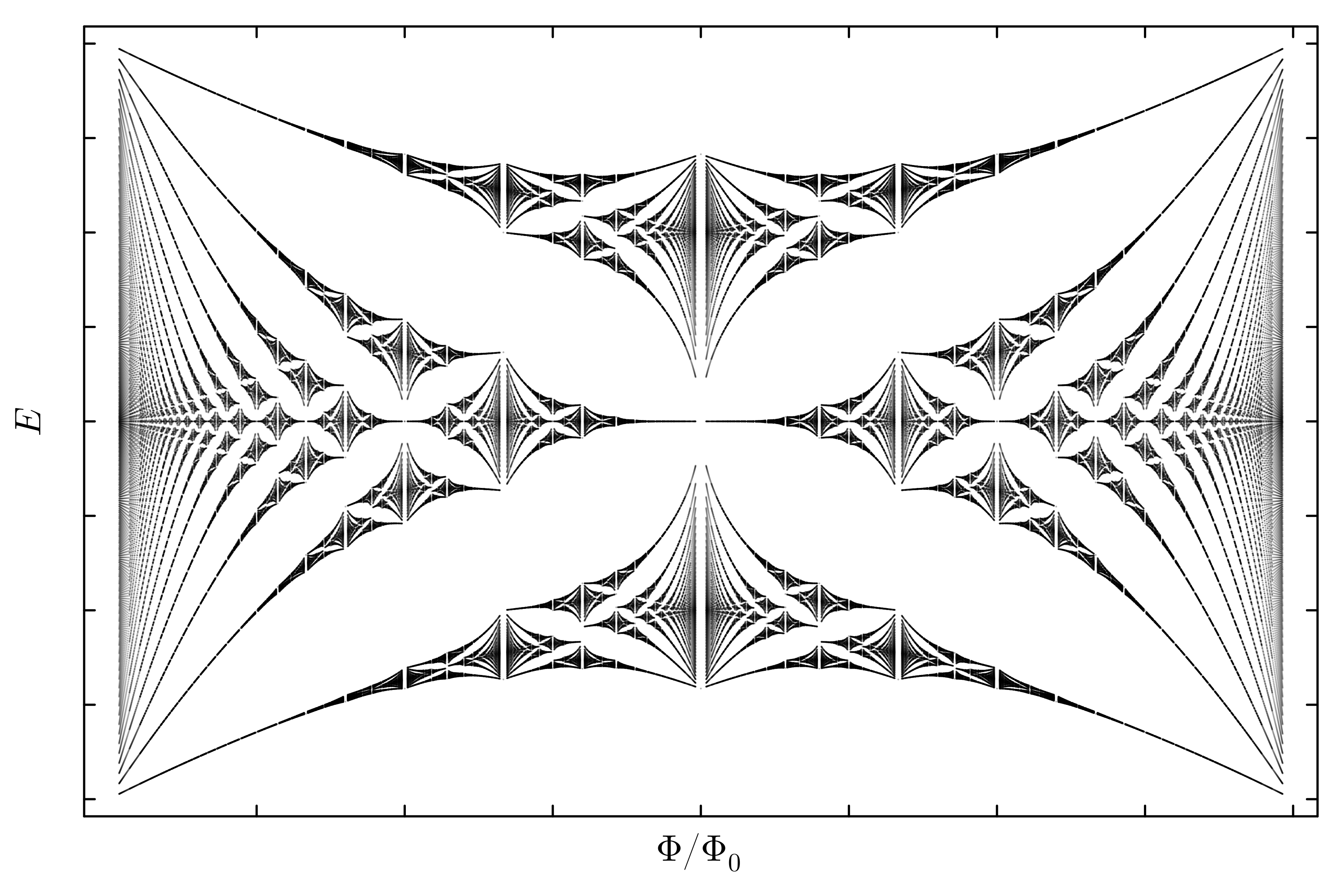
Goal
The goal of this project is to develop a general theoretical understanding of a 2D realization of the system discussed above, using a blend of theory and numerics. After a comprehensive introduction to cold atom physics and the quantum Hall effect, we will first examine the non-interacting case. A particularly interesting direction is exploring how the center-of-mass motion reflects the non-trivial topological properties of the band spectrum, as demonstrated in a remarkable experiment on a different system [6]. A key question to address in this context is the state preparation process. With a solid understanding of the non-interacting regime, the student can explore the effects of including weak interactions. The setup inherently gives rise to long-range anisotropic interactions, which are expected to lead to exotic ground-state physics. The field of cold atom physics thrives on the synergy between theory and experiment; therefore, this project is ideal for students with a strong interest in both theoretical and experimental physics, especially those eager to explore exotic quantum phenomena and engage in interdisciplinary physics research.
[1] Zhang et al., (2018) arXiv:1810.09228
[2] Dalibard, (2015) arXiv:1504.05520
[3] Price et al., (2016) arXiv:1605.09310
[4] Oliver et al., (2021) arXiv:2112.10648
[5] Reid et al., (2024) arXiv:2410.10501
[6] Aidelsburger et al., (2014) arXiv:1407.4205